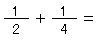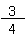ここでは、「小数」と「分数」を説明するよ。
「分数」ってなぁに?
リンゴは、1コ、2コって数えるよね。では、下の問題を考えよう。
半分に切ったリンゴ1つは、もとのリンゴのいくつ分の大きさでしょうか?
まずは、図を描いてみよう。
1コのリンゴを、包丁で、半分にしたから、こんな感じかな。

半分のリンゴは2コになったね。
大きさを比べやすいように、リンゴを丸に描き替えよう。
こんな感じかな。分かりやすいように色も少し変えているよ。

では、半分に切ったリンゴ1つと、もとのリンゴの大きさを比べてみよう。
さっきの絵を重ね合わせるよ。

当然だけど、半分のリンゴ2コを合わせると、もとのリンゴ1コと同じ大きさだよね。
では、さっきの問題を考えてみよう。
「ちょうど二つに分ける」ことを、「ニ等分にする」っていうんだ。
これを使って言いかえると、答えは、
算数では、「二等分にしたときの、1コ分」を、「2分の1」っていうんだ。
よみかたは「に ぶんの いち」だよ。
これを使って言いかえると、答えは、
算数っぽい答えで、カッコいいね。
でも、もっとカッコいい書き方はないかな?
実は、「2分の1」を記号で書くことができるんだ。
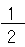 になるんだ。
になるんだ。このように書く数を「分数」って呼ぶんだ。
分数を書くときは、真ん中に線を引いて、下には「2分の1」の「2」を、上には「2分の1」の「1」を書くんだ。
図で書くとこんな感じかな。
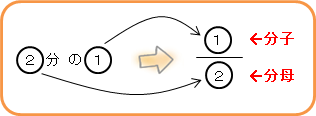
分数は上の数字と下の数字に読み方があるんだ。
上の数字を分子(ぶんし)、下の数字を分母(ぶんぼ)って呼ぶんだ。
ちなみに、真ん中の線を「括線」(かっせん)と呼ぶんだ。
「分数」ってなぁに?(2)
さっきは、リンゴで考えたけど、ここでは図を使って考えよう。
分数は、元の大きさを「1」として考えるんだ。
さっきのリンゴでは、リンゴ1コを「1」として考えたんだよ。
「1」とする大きさは何でもいいんだ。
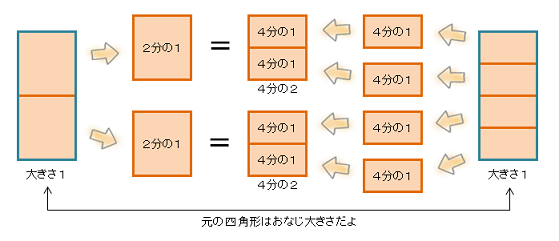
下の図で、もとの四角形を「1」とするよ。
四角形を二等分したときの、1個の大きさを「2分の1」というんだ。
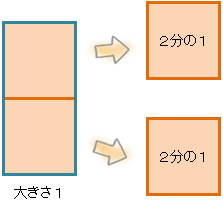
「○分の△」の、○には「1の大きさをいくつに分けたか」を書き、△には「分けたものをいくつ集めたか」を書くんだ。
式にするときは、「○分の△」の○を分数の分母に、△を分数の分子に書くんだ。
図で書くとこんな感じかな。

分数は上の数字と下の数字に読み方があるんだ。
上の数字を分子(ぶんし)、下の数字を分母(ぶんぼ)って呼ぶんだ。
ちなみに、真ん中の線を「括線」(かっせん)と呼ぶんだ。
四角形を四等分したときの、1個の大きさを「4分の1」といい、式で書くと、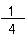 だ。
だ。
「4分の1」を2個合わせると、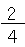 で、「2分の1」と同じ大きさになるんだ。
で、「2分の1」と同じ大きさになるんだ。
図で書くとこんな感じかな。
「分数」ってなぁに?(3)
では、分数を使ってみよう。
分数を使うことで、もっと分数のことが分かってくると思うよ。
下の問題を考えよう。
扇(おうぎ)型のケーキ1コは、もとのケーキの、何分の1の、大きさでしょうか?
はじめに、図を書いて考えよう。
ケーキを、扇型に、四等分に、切り分けているから、図を書くとこんな感じかな。
ケーキは赤い丸で、点線がナイフで切ったところだよ。
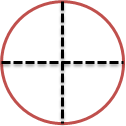
扇(おうぎ)型のケーキ1コは下のような形になるね。
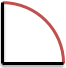
たとえば、下の赤色の図形が、扇型だよ。

さて、もとのケーキがいくつに分かれたかな?
そう、四つだよね。ケーキを「四等分」に切ったんだから、四つだよね。
扇型のケーキ1コは、「四等分にしたときの、1コ分」だから、
扇(おうぎ)型のケーキ1コは、もとのケーキの、何分の1の、大きさでしょうか?
式で書くと、
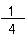
下の問題を考えよう。
扇(おうぎ)型の ケーキ2コ は、もとのケーキの、何分の1の、大きさでしょうか?
ケーキを、扇型に、四等分に、切り分けているから、図を書くとこんな感じかな。
ケーキは赤い丸で、点線がナイフで切ったところだよ。

さっきの問題で答えたように、扇形のケーキ1コは、もとのケーキの4分の1の大きさだよね。
今回は、
「4分の2」でも間違っていないんだけど、小さな数を使って書き換えることができるんだ。
小さな数で書き換えると見やすくなるから、とても便利なんだ。
たとえば、「100000分の50000」よりは「2分の1」の方が見やすいでしょ。
では、どんな数で書き換えられるか考えよう。
ケーキを切った図に、4分の2を書き込んでみるよ。
赤い線が、4分の2だよ。
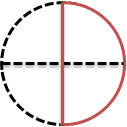
もしかして、ケーキの半分じゃないかな?!
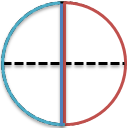
青い線で囲んだ扇型のケーキは2コだから、4分の2の大きさだよね。
あ、赤い線と青い線は、同じ大きさだよね。
つまり、赤い線の大きさは、ケーキを、2等分したときの1コ分、と同じ大きさだよね。
いいかえると、赤い線の大きさは、もとのケーキの2分の1の大きさだよね。
あれ? さっき答えは「4分の2」だったけど「2分の1」になったね。
間違いじゃないよ。
「4分の2」と「2分の1」は同じ大きさなんだ。
だから、「4分の2」は「2分の1」に書き換えていいんだ。
小さな数で書き換えるために、毎回、図を書くのは大変だよね。
記号を使って計算する方法を考えてみよう。
はじめに、ケーキを2等分、4等分、8等分と、分ける数を2倍ずつにして、分けた数の半分の個数の大きさを考えてみよう。
はじめは、2等分するよ。
2コに分けたから、その半分の1コ分の大きさを考えるよ。
図の赤い図形だね。
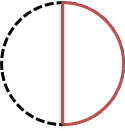
おおきさは、「2分の1」だよね。
つぎに、4等分にしてみよう。
4コに分けたから、その半分の2コ分の大きさを考えるよ。
図の赤い図形だね。
ちなみに青い図形は「4分の1」だよ。
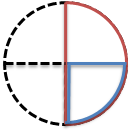
図の赤い図形の大きさは、「4分の2」だよね。
これは、「2分の1」と同じ大きさだよね。
つまり、「4分の2」は「2分の1」に書きかえることができるんだね。
つぎに、8等分にしてみよう。
8コに分けたから、その半分の4コ分の大きさを考えるよ。
図の赤い図形だね。
ちなみに緑の図形は「8分の1」だよ。
青い図形は「4分の1」だよ。
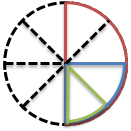
図の赤い図形の大きさは、「8分の4」だよね。
これは、「4分の2」や「2分の1」と同じ大きさだよね。
つまり、「8分の4」は「4分の2」と「2分の1」に書きかえることができるんだね。
さて、下に書きかえた数を、まとめてみたよ。
・8分の4 = 4分の2
= 2分の1
・「○分の△」で、○が2倍になると、△も2倍になる。
もう、気が付いたかな。
「○分の△」の○と△を、同じ数でわり算しても、かけ算しても、大きさは同じになるんだ。
たとえば、
「4分の2」は「2分の1」と同じだったよね。
「8分の4」は「2分の1」と同じだったよね。
次は、わり算してみよう。
たとえば、
「○分の△」の○と△を、同じ数でわり算してもかけ算しても、大きさは同じになることは大事なことだから、覚えておこう。
分数の記号で考えてみよう。
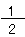
・4分の2は、
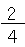 =
=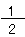
・8分の4は、
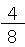 =
=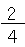
=
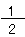
もう、気が付いたかな。
分母と分子を、同じ数でわり算しても、かけ算しても、大きさは同じになっているね。
たとえば、
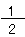 の分母「2」と分子「1」を2倍にすると、
の分母「2」と分子「1」を2倍にすると、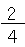 になるよね。
になるよね。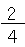 =
=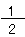 、だったよね。
、だったよね。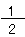 の分母「2」と分子「1」を4倍にすると、
の分母「2」と分子「1」を4倍にすると、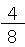 になるよね。
になるよね。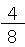 =
=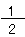 、だったよね。
、だったよね。次は、わり算してみよう。
たとえば、
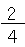 の分母「4」と分子「2」を、2で割ると、
の分母「4」と分子「2」を、2で割ると、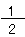 になるよね。
になるよね。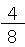 の分母「8」と分子「4」を、4で割ると、
の分母「8」と分子「4」を、4で割ると、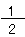 になるよね。
になるよね。分母と分子を、同じ数でわり算しても、かけ算しても、大きさは同じになることは大事なことだから、覚えておこう。
ちなみに、「分母と分子を、同じ数でわり算する」ことを「約分する」というんだ。
「約分」って言い方はカッコいいよね。忘れずにおぼえておこう。
「小数」ってなぁに?
長さはメートルやキロメートルを使って表すよね。たとえば、100m、500m、もっと長くなると、10,000mや50,000mにもなるよね。
10,000mや50,000mをキロメートルにすると、10kmや50kmになるよね。(1,000mは1kmだからね)
桁数が少なくなって見やすくなるよね。
ところで、10,500mの場合は何kmだろう?
1,000mは1kmだから、10k500mだね。
500mもkmを使って書けないかな?
実は、数には「小数」っていうのがあるんだ。
1kmと2kmの差は「1」kmだよね。
その「1」を10等分にしたとき、その1コ分を「0.1」(れー てん いち)と書くんだ。
分数でいうと、「1」の10分の1を「0.1」と書くんだ。
式で書くと、
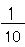 = 0.1なんだ。
= 0.1なんだ。0.1の次は0.2、0.3と増えていくよ。0.9の次は1だよ。
図を書くとこんな感じかな。

小数はどこでも使えるよ。たとえば、0から2までを書くとこんな感じかな。

「1.1」や「1.2」の「.」(てん)は、「小数点」というんだ。
そして、「1.1」や「1.2」のように、「小数点」がある数を「小数」というんだ。
さて、さっきの、
100mは、「1,000mの10分の1」だよね。
ということは、100mは、「1kmの10分の1」って書けるよね。
これを計算すると、100mは、「0.1km」になるよね。
だから、500mは、「0.5km」だよね。
それでは、
つぎの問題を考えてみよう
1メートルは、100cmだよね。
だから、2.56mの中の、2mは200cmだよね。
残りの、0.56mの中の、0.5mは、何cmだろう?
0.1mは、1mの10分の1だから、
0.1mは、100cm÷10
0.1mは、10cm
だから、0.5mは、50cmだよね。
残りの、0.06mは、何cmだろう?
0.01mは、0.1mの10分の1だよね。
だから、0.01mは、10cmの10分の1になるよね。
だから、0.01mは、1cmだよね。
だから、0.06mは、6cmだよね。
だから、2.56mは、256cmだよね。
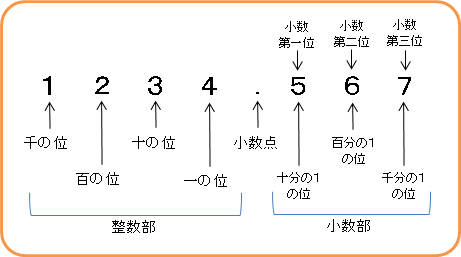
小数には、桁によって呼び方があるんだ。
小数では、小数点の左を整数部、右を小数部っていうんだ。
たとえば、「2.56」の整数部は「2」だね。
小数点のすぐ右の桁を、小数第一位というんだ。
「2.56」の小数第一位は「5」だね。
小数第一位は、10分の1の大きさなんだ。
小数第一位の右の桁を、小数第二位、その次を小数第三位っていうように続くんだ。
「2.56」の小数第二位は「6」だね。
小数第二位は、小数第一位の10分の1の大きさなんだ。
言い換えると、小数第二位は、100分の1の大きさなんだ。
「小数」を計算しよう
小数を計算するときは、整数部と整数部、小数部と小数部を足すようにして計算するんだ。
ひっ算で計算するときは、小数点の位置を合わせて書いて、計算するんだ。
たとえば、「1.1」に「0.1」を足すときは、
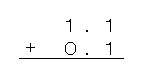
のように書くんだ。
計算するときは、たし算と同じように、列ごとに計算するんだ。
これを計算すると、
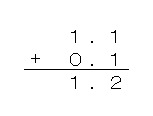
になるね。
「分数」を計算しよう
分数のたし算
分数のたし算とひき算は、分母をそろえてから、分子をたし算やひき算して計算するんだ。
「分母をそろえる」ことを、「通分(つうぶん)する」というんだ。
それでは、次の、分数のたし算を計算してみよう。
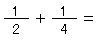
はじめに、通分する(分母をそろえる)よ。
小さい数の方が見やすくて、計算しやすいよね。だから、分母は、最小公倍数にそろえよう。
「2」と「4」の最小公倍数は「4」だよね。
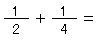
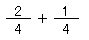
次に、式を変形しよう。式が変形するなんて、おもしろいよね。
分数のたし算とひき算では、分母が同じときは、分母を一つにして、分子には、それぞれの分数の分子を書いていいんだ。
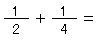
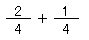
=
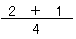

次に、分子を計算しよう。
「2+1」を計算するよ。
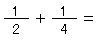
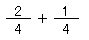
=
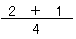
=
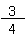
だから、答えは、